哈希
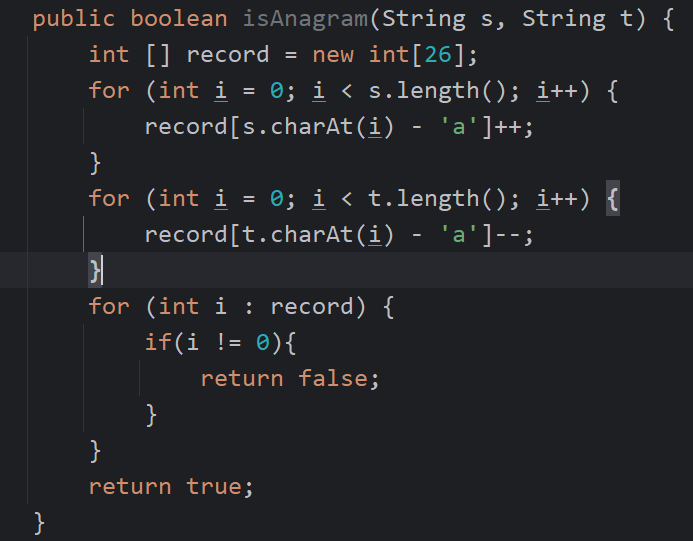
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1: 输入: s = “anagram”, t = “nagaram” 输出: true
示例 2: 输入: s = “rat”, t = “car” 输出: false
说明: 你可以假设字符串只包含小写字母
- 思路: 思路就是将不同字母的个数存放在同一数组的相同位置上,这其实就是哈希思想,哈希是通过哈希函数映射的,而在本题中
,可以直接借助字母的阿斯克码值,即定义新的数组,长度为所有字母长度,字母a的个数为新数组的索引0,然后将字符串中出现的
字母与a相减得到在新数组中的坐标,这样也不会重复。
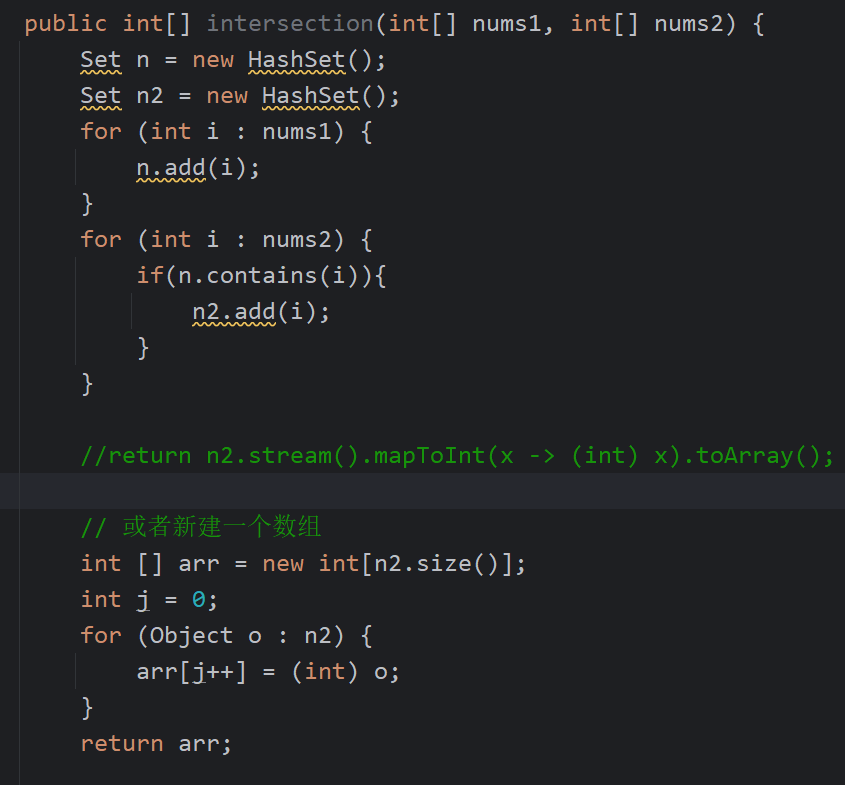
两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的
交集
。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
- 思路: 用到了哈希相关知识—— set结构,set结构是不允许重复的,所以相同的元素只会存一次,因此本题可以将数组里的数依此放入
到set里,之后依此遍历另一个数组,并再次调用set里的函数判断是否包含相应的数字。返回结果为数组,可将set以流的形式转换为数组输出。
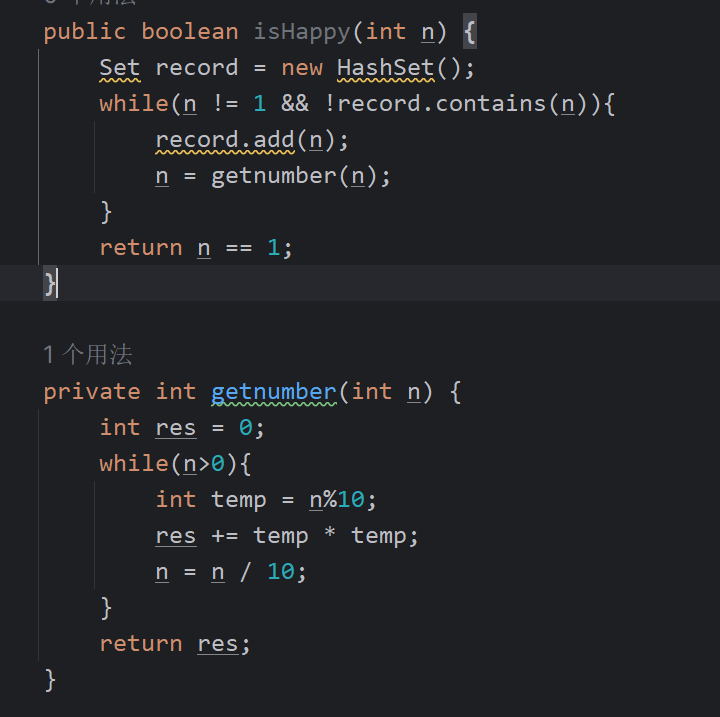
快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
- 思路:重点是判断 每次结果是否为1,以及已经出现过的数字是否重复出现。后者就用到了哈希,建立一个新的哈希列表,每次将结果放进去,然后在循环终止条件上加入
是否重复出现。
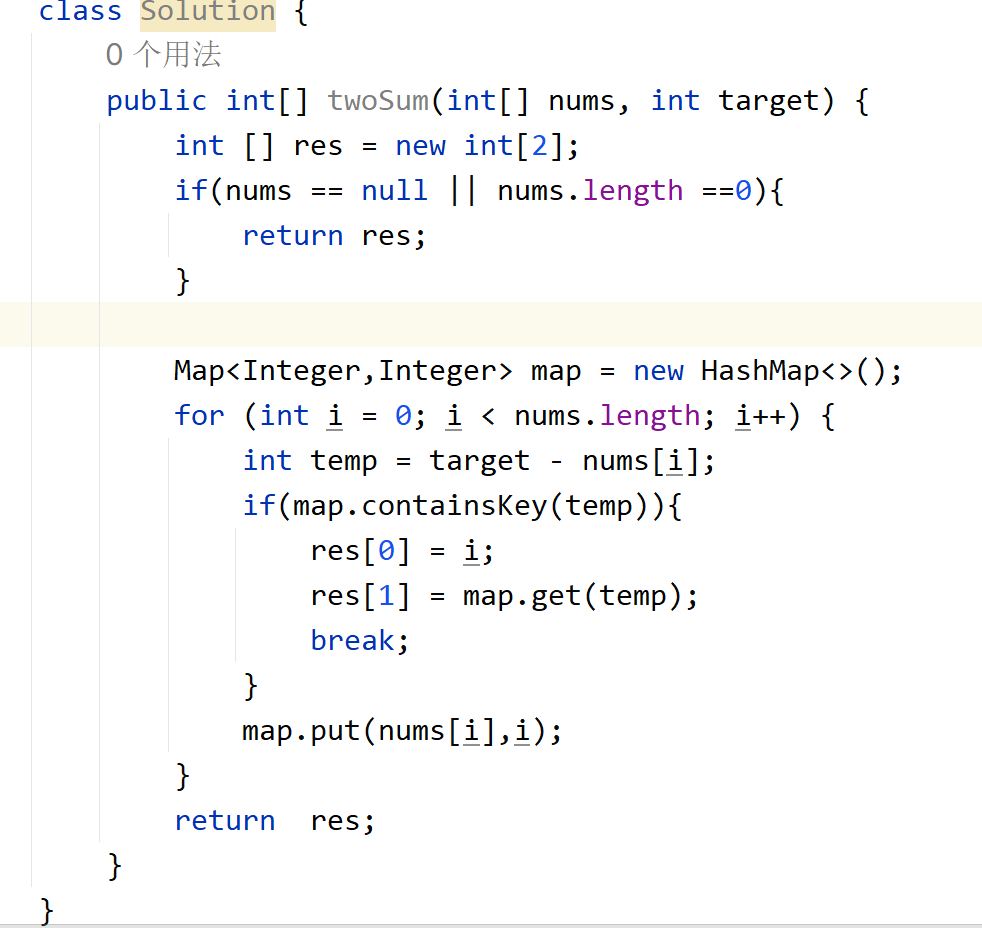
两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
- 思路:如果用到不允许重复的条件可以考虑哈希,本题就是,只要将目标数与数组内的每一个数相减,如果这个差数出现在map中,就找到了这么一对。
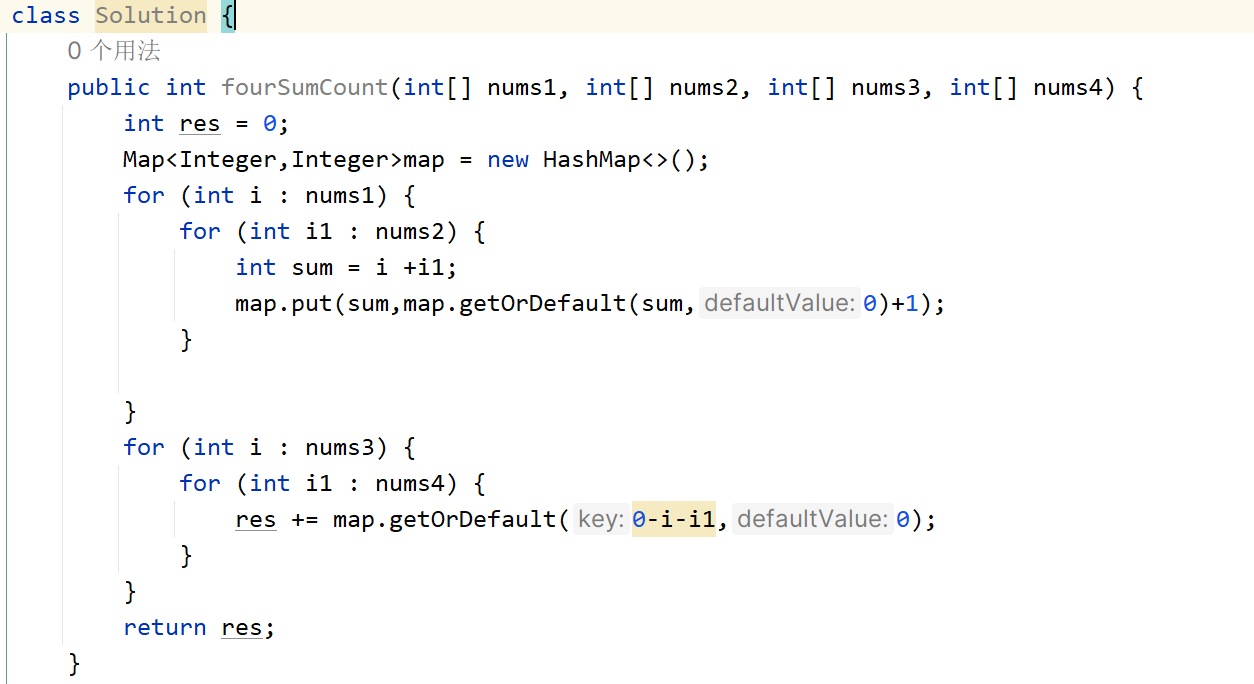
四数相加
给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足:
0 <= i, j, k, l < n
nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0
- 思路:与上题一样,都是拿着现有的数去哈希里找目标数,因为是只计算多少组,即只计算个数就行,所以对半分,先遍历
前两个数组,将它们的和写入哈希中,将他们出现的次数作为value值,然后用最终求和的数减去后两个数组遍历的值,
放入到哈希里查找出现的个数。所有个数相加就可得到最终结果。
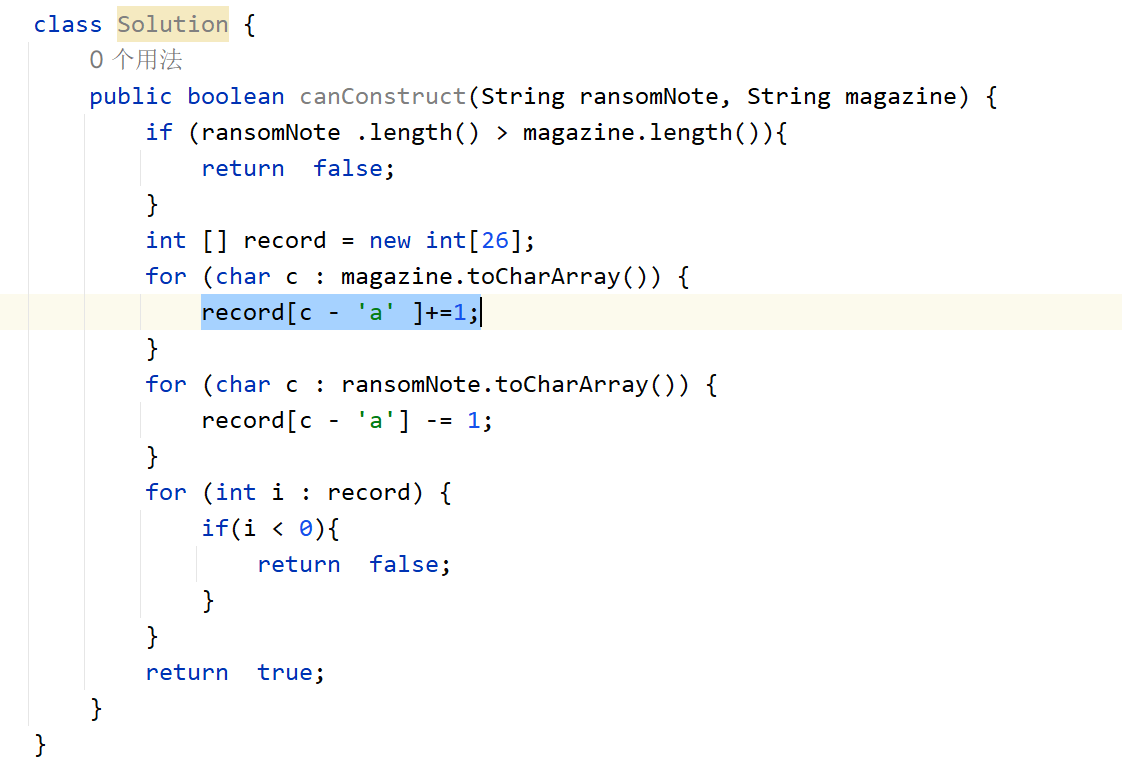
赎金信
给定一个赎金信 (ransom) 字符串和一个杂志(magazine)字符串,判断第一个字符串 ransom 能不能由第二个字符串 magazines 里面的字符构成。如果可以构成,返回 true ;否则返回 false。
(题目说明:为了不暴露赎金信字迹,要从杂志上搜索各个需要的字母,组成单词来表达意思。杂志字符串中的每个字符只能在赎金信字符串中使用一次。)
- 思路:优先想到的是map,但是用map内部要维护红黑树和链表,还要构建哈希函数,开销较大,所以利用哈希思想,建立一个长度为26
的列表,后一个字符串内的每一个字母出现一次就对应加1,拿着这个数组,前一个数组每出现一个字母,对应减1,这样只要出现小于0的,就说明
不符合。能这样用是因为字母本身就是一个kv,k是它们的先后顺序。
三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有满足条件且不重复的三元组。
- 思路: 利用了双指针,因为要求不能重复,所以要注意的点就是去重,先说双指针,遍历数组,将左指针安排在遍历值的前一个,右指针安排在数组最后,
以三者之和为判断标准,大了右指针左移,小了左指针右移,刚好和为0就写入结果内,接下来就是去重,需要去重的地方对应三个数,遍历的数的地方,要抱枕
自己的值不能和上一个值相同,左右指针处的值要保证不能和下一个值相同。 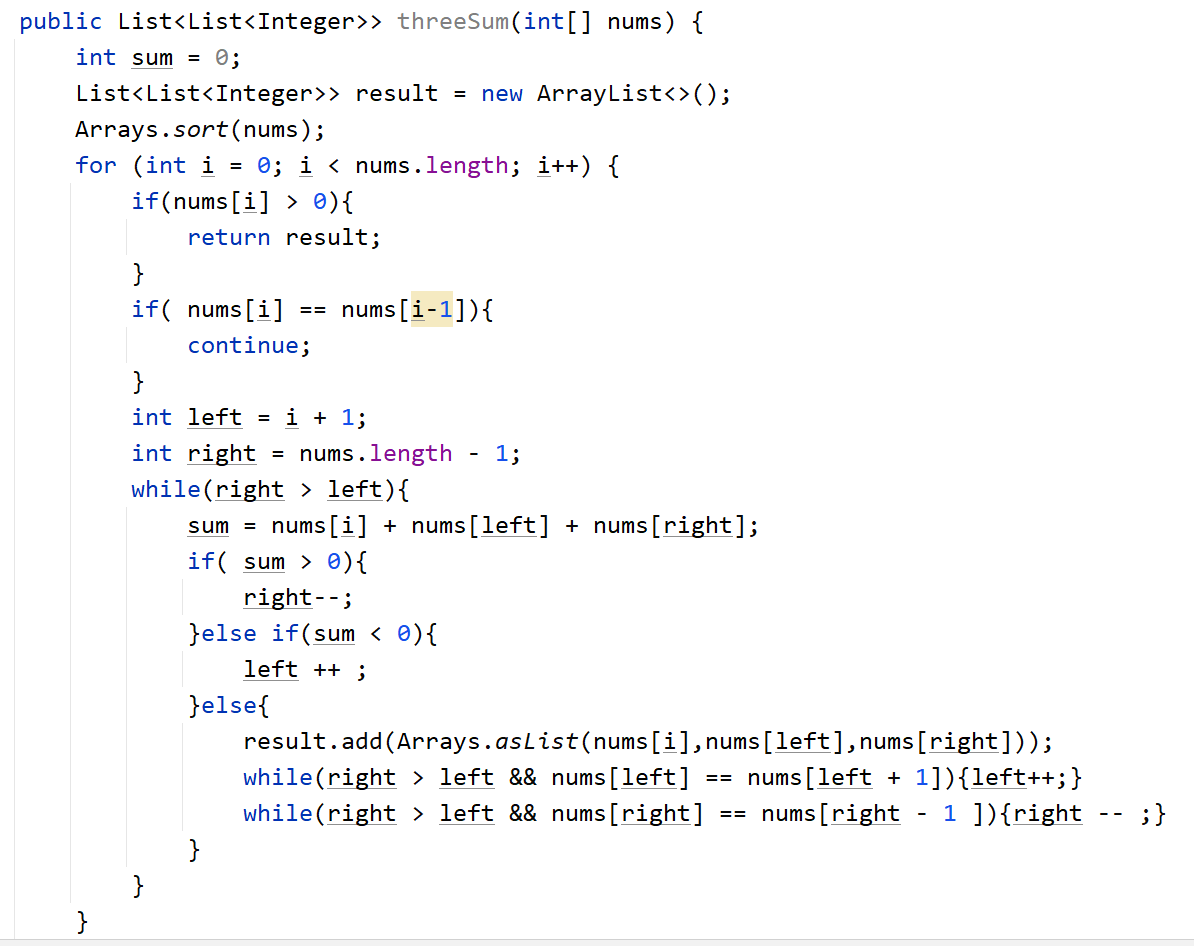
四数之和
跟上述题目描述基本一致。直接说思路
- 思路:其实就是三数之和的思路,在三数之和的基础上加一个for循环,内部一样的还是双指针。
