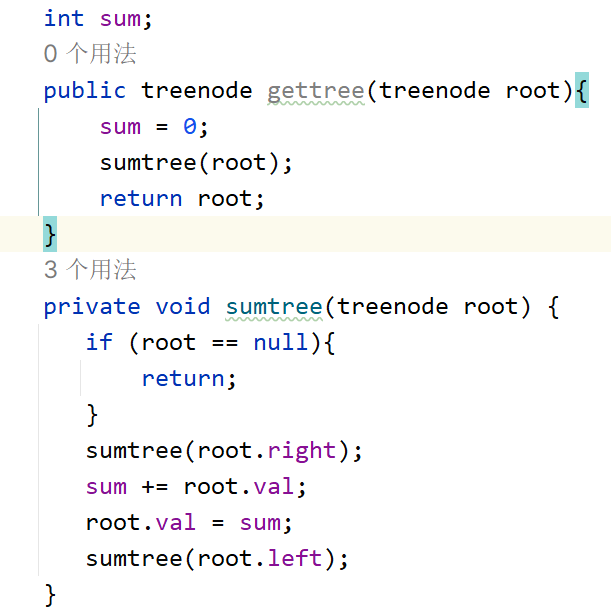
二叉树

遍历

• 前序遍历：用到了递归，设置好递归的参数值，终止条件，然后递归查询，前中后的遍历方式就是将查询到的值放入的位置不同。

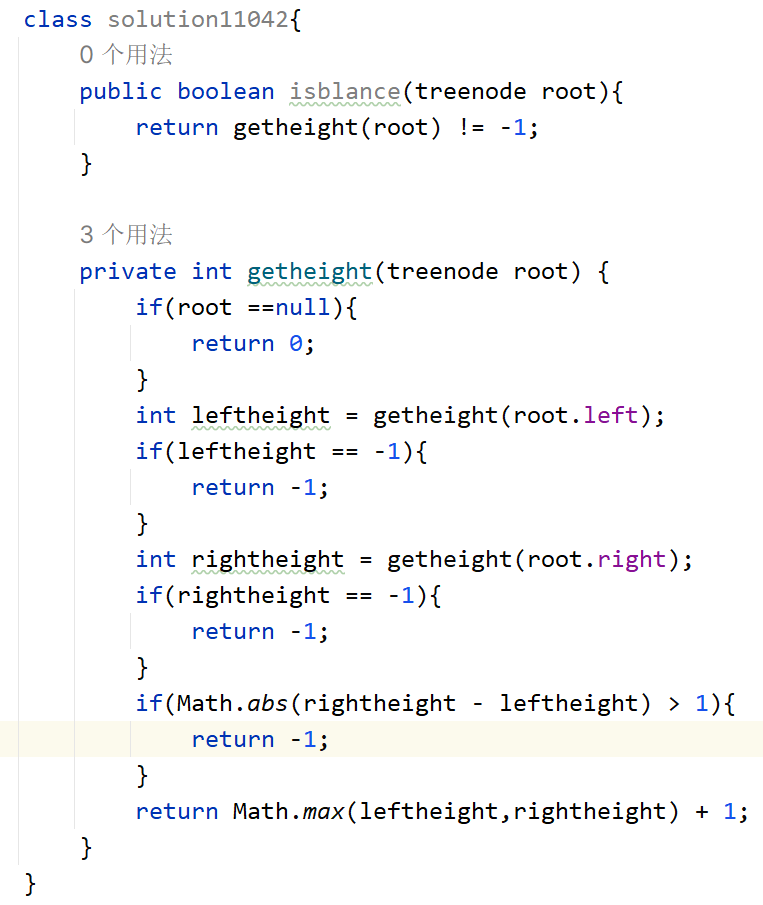
层序遍历

将二叉树按层遍历

• 思路： 先定义一个队列，把根节点放入其中，然后按照队列长度为循环次数，依此遍历节点的左右节点到队列中
  ，这是一个模板，靠这个可以解决下面的问题：
  • 遍历二叉树右视图，遍历步骤不变，变的是提取节点，只提取右节点，因为放入队列中的时候右节点是在队列的右边，
    所以，只需要取队列最后一个元素即可。
  • 二叉树的平均值，最大值，同样返回对应的运算结果即可。
  • N叉数层序遍历，只是多了多个孩节点，步骤不变。
  • 填充每个节点的下一个右侧节点：遍历到队列中，一边放孩节点，一边更改指向的下一个节点。
  • 最大深度： 遍历然后记录深度，也就是遍历的次数
  • 最小深度： 判断遇到无子节点的，然后返回此时的深度，即为最小深度。

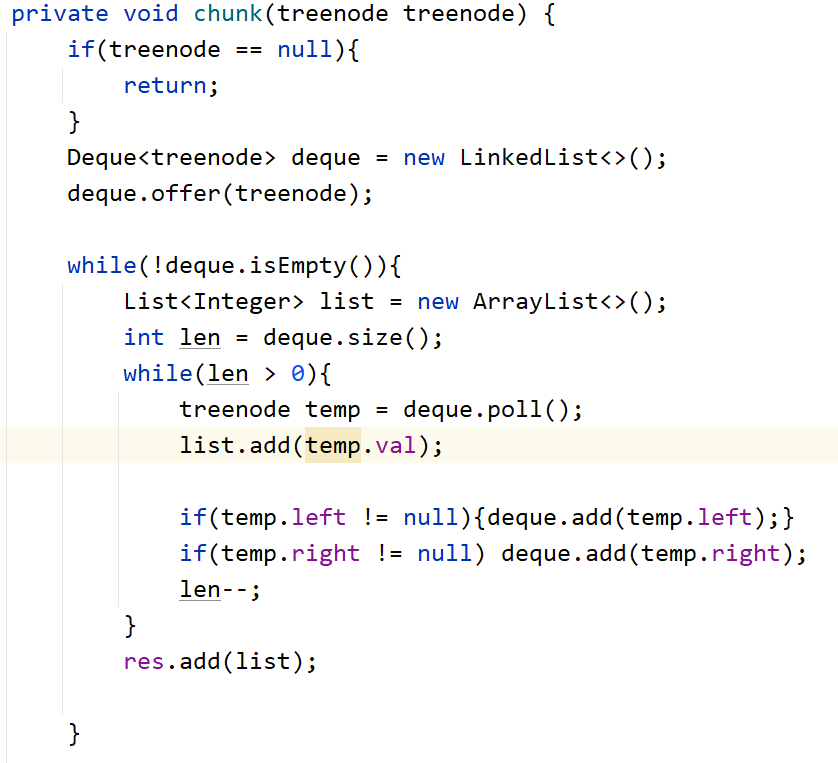
反转二叉树

翻转一棵二叉树。

• 思路：递归实现，写出反转逻辑，及就是交换左右节点，然后靠递归实现左右两半的各自反转。

对称二叉树

给定一个二叉树，检查它是否是镜像对称的

• 思路，归根结底还是比较节点是否相同，所以就要用到递归，递归内就是节点的比较，递归的参数就是要比较的节点，从根节点开始
  ，依此向下比较。

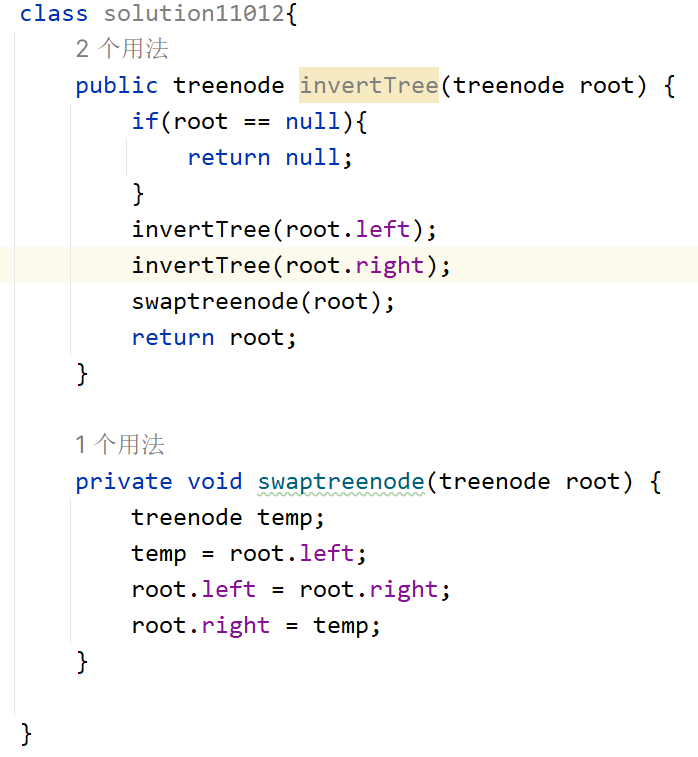
平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

• 思路： 同样比的是每一个节点，所以还是用递归，递归内是比较该节点的左右子节点是否高度差大于1，不大则返回节点最大深度。

二叉树的所有路径

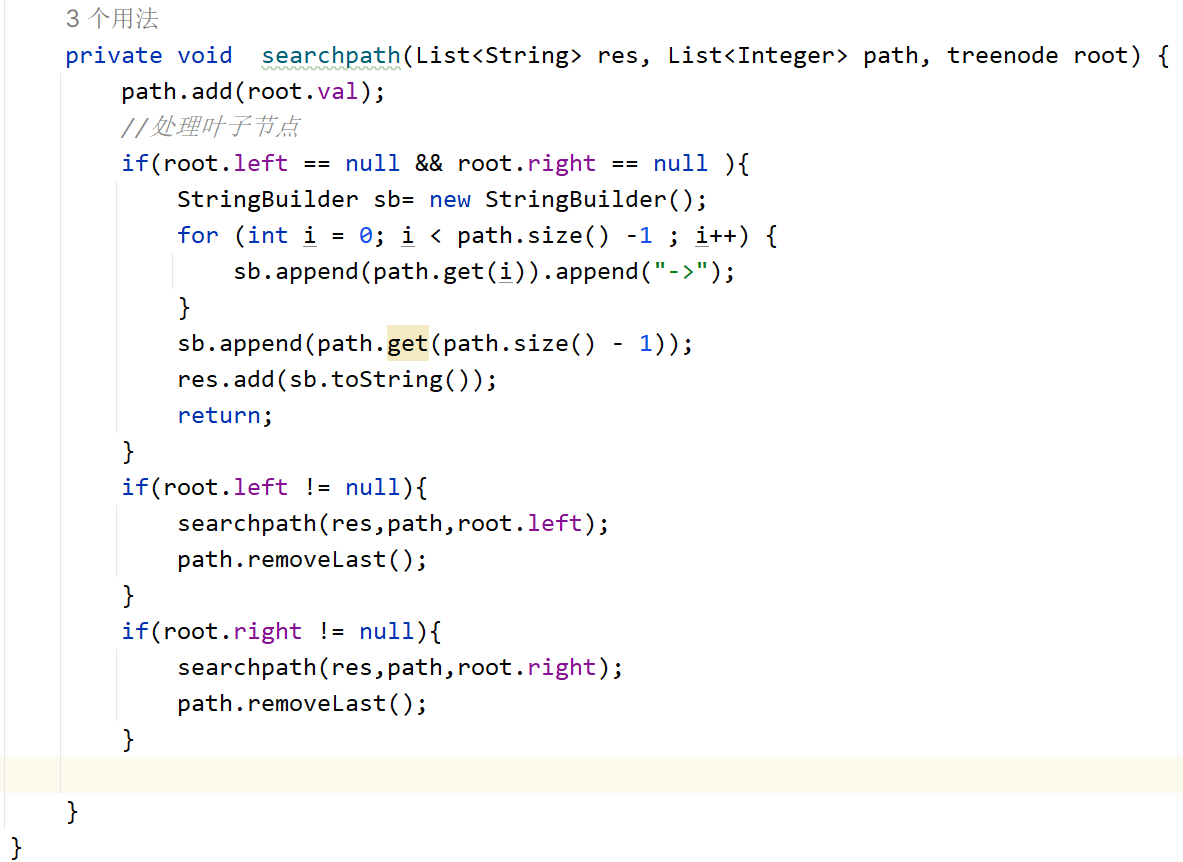
给定一个二叉树，返回所有从根节点到叶子节点的路径。

• 思路：递归加回溯，遍历每一个节点，递归内是叶子节点就整理路径并加入结果列表，不是叶子节点就递归到叶子节点，然后回溯到当前节点。

左叶子之和

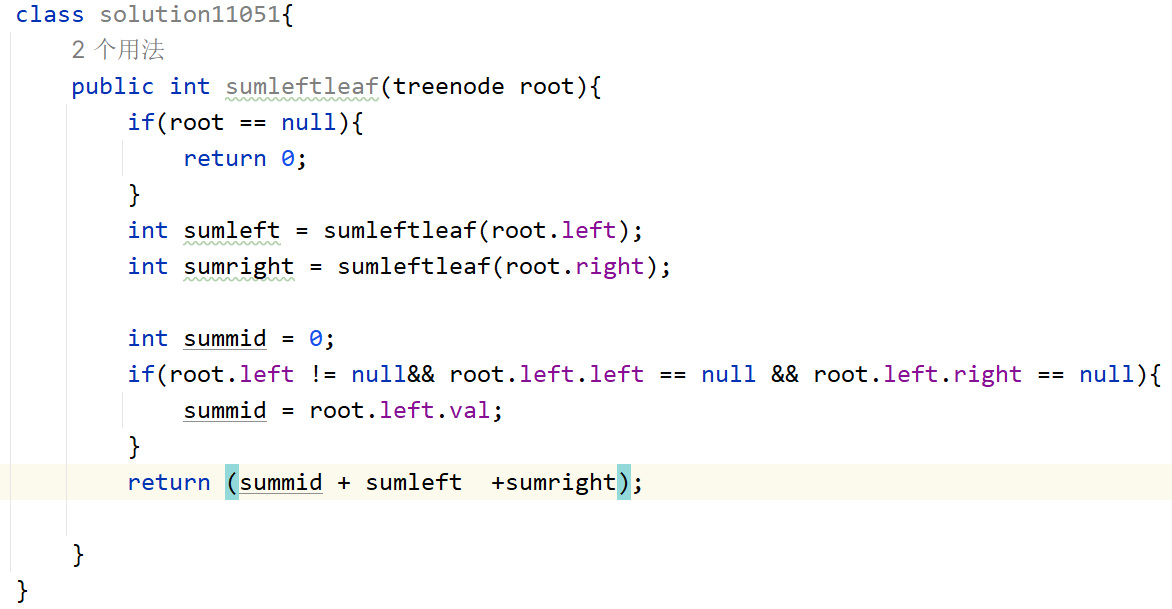
计算给定二叉树的所有左叶子之和。

• 思路：依旧是递归，递归内部是计算各自对应的左叶子之和，也就是将根节点一分为二，然后判断是不是叶子节点，是则相加。

找树左下角的值

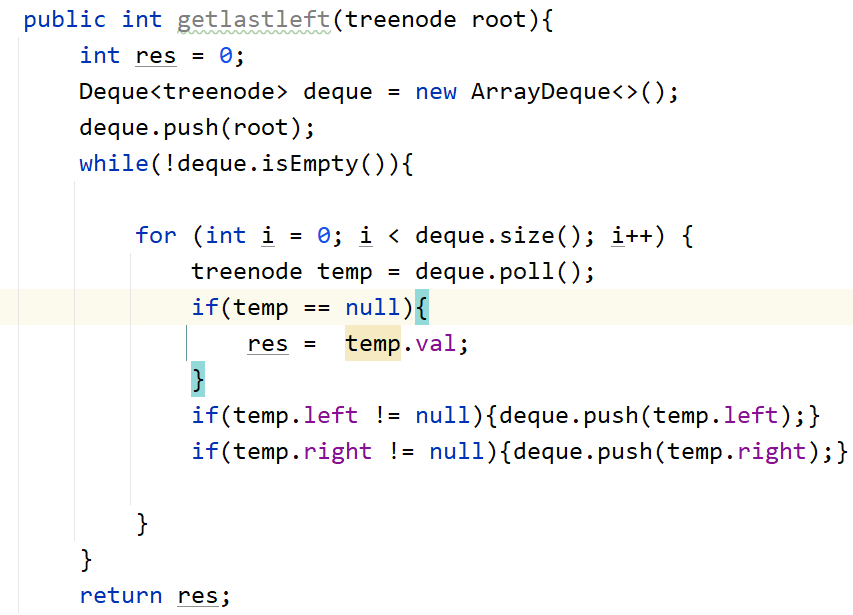
给定一个二叉树，在树的最后一行找到最左边的值。

• 思路：层序遍历,将节点压入栈中，最后一个弹出的就是最左边的值，当然要保证放入栈的顺序为先左后右。

路径总和

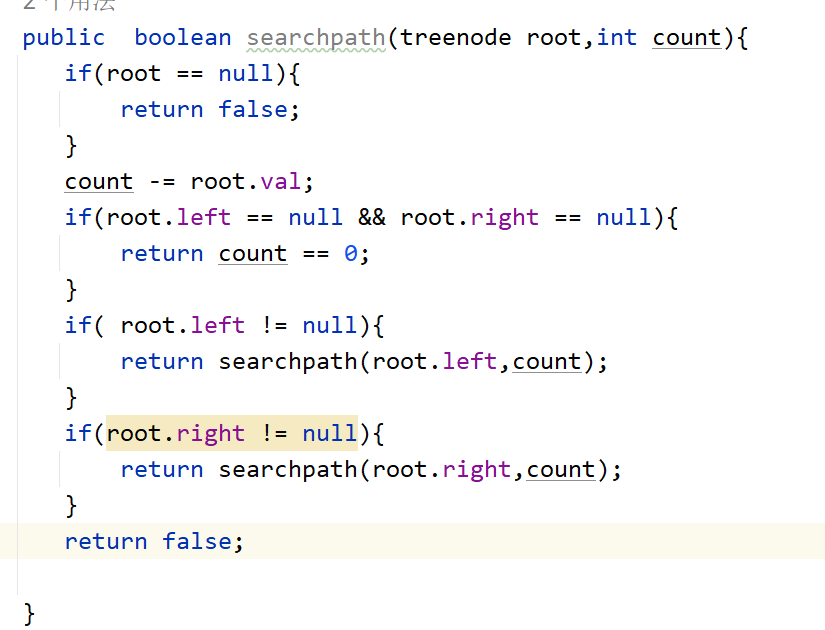
给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

• 思路： 只是判断是否找到，所以可以拿目标数逐个减，同样在叶子节点做判断，不是叶子节点就递归。

根据中序遍历与后序遍历构造二叉树

根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

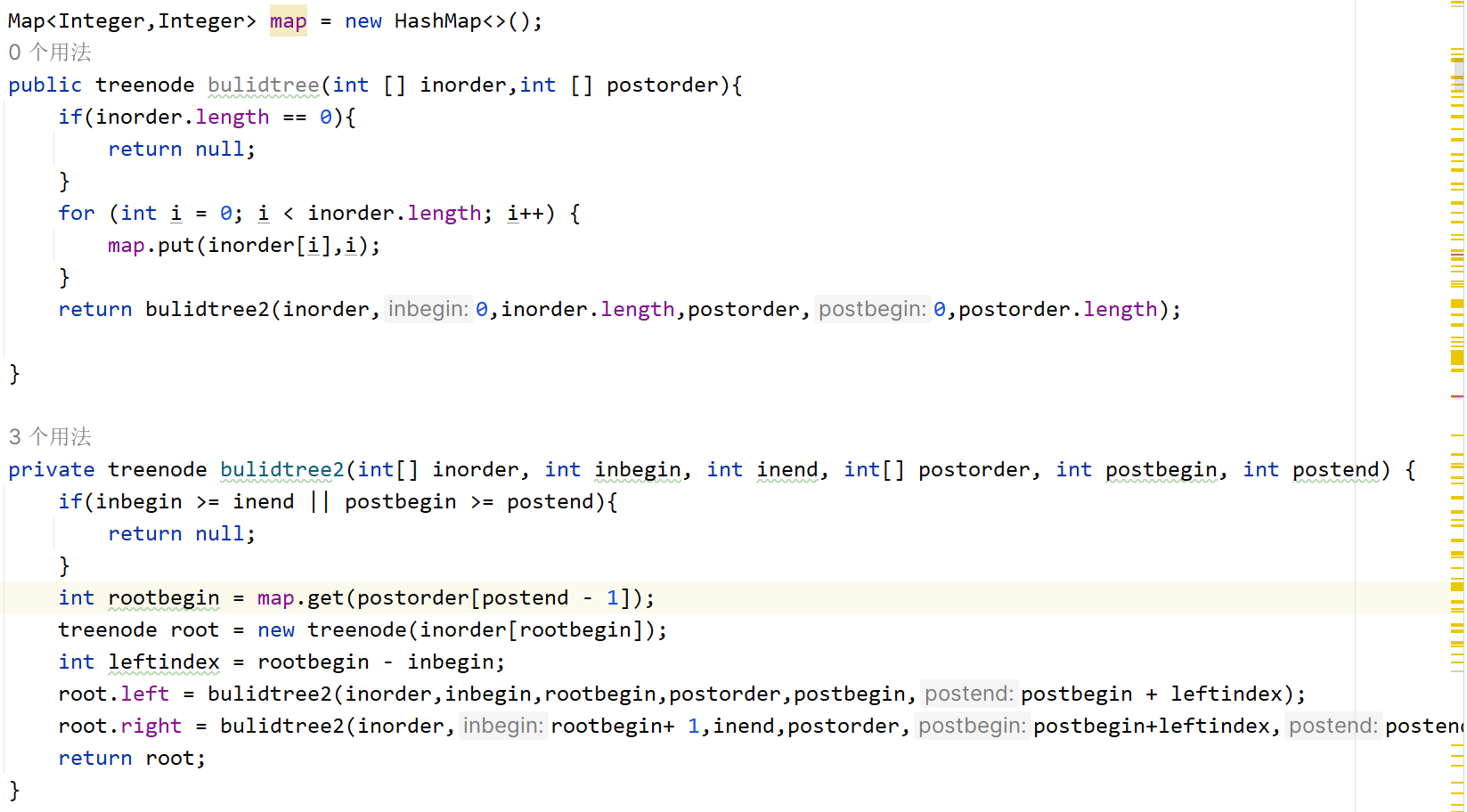
• 思路： 后序遍历的最后一个元素为根节点，所以可以根据根节点在中序遍历中找到左右节点，按照该元素划分中序遍历，之前为左，之后为右
  ，同样用到了递归，递归内建立新节点，新节点的左右节点通过递归获得。提前将中序遍历的内容放入map可方便后续查找其元素对应的索引。

最大二叉树

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：
二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树，并且输出这个树的根节点。

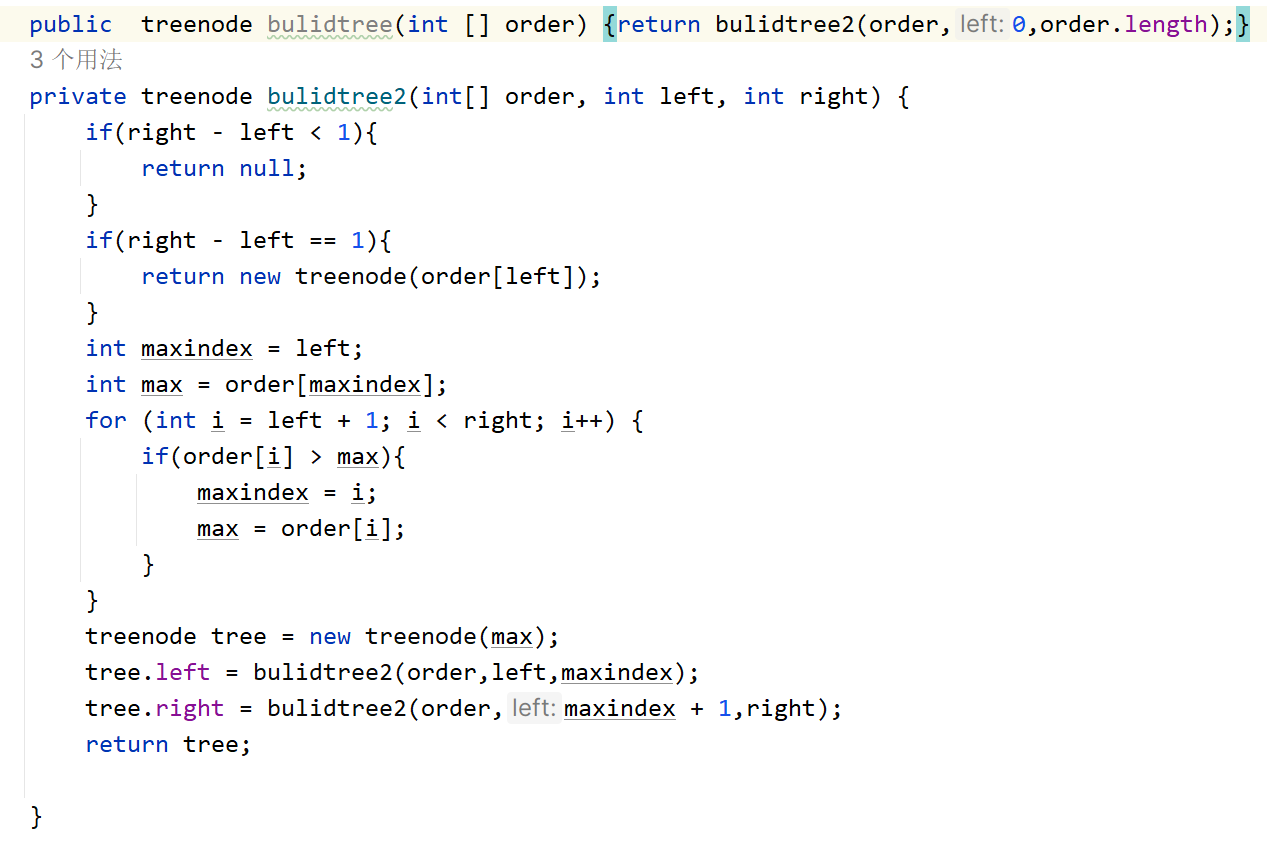
• 思路：同样是递归，递归终止条件是左右区间不正常，左右区间小于1就返回空值，为1就返回节点，否则就还是区间，那么就开始
  找最大值及其对应下标，然后将最大值建立为新节点，新节点的左右节点再通过递归获得。递归参数就是数组以及其左右区间。

合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

• 思路：递归，每一个新节点的产生就是原本的两个二叉树的节点的输入，一个为空就返回另一个，都不为空就返回相加的结果。

搜索二叉树

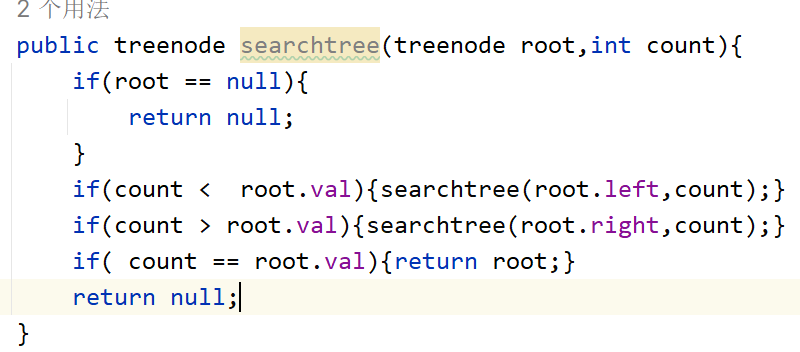
给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL

• 思路：因为是二叉搜索树，所以就可以拿目标数与节点值进行比较，大于递归传入右节点，小于递归传入左节点。相等返回该节点。

验证二叉搜索树

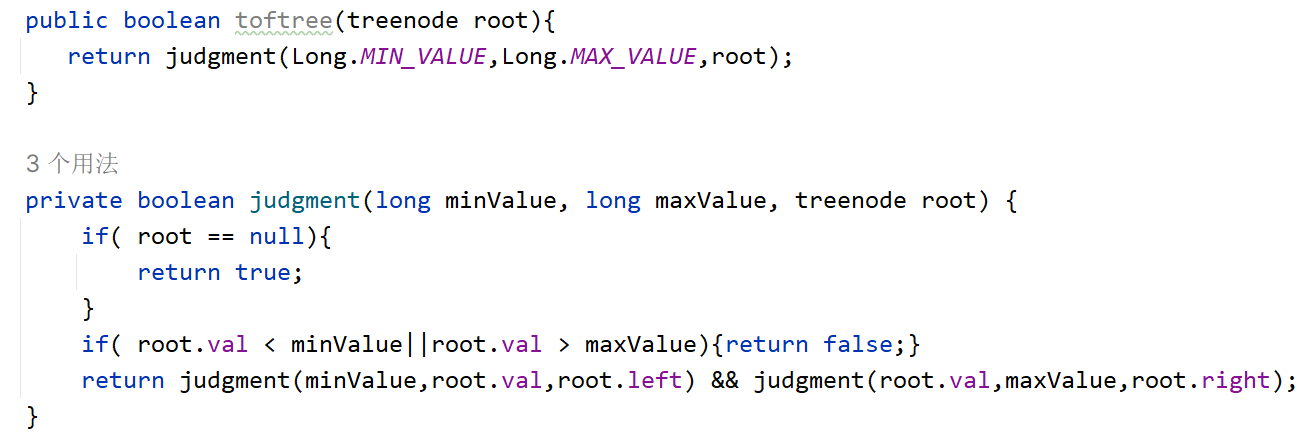
给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

• 思路：递归的思想，直接用子节点的值比较容易报空值异常，所以应该拿子节点去和根节点的值和最大最小值进行比较。

二叉搜索树的最小绝对差

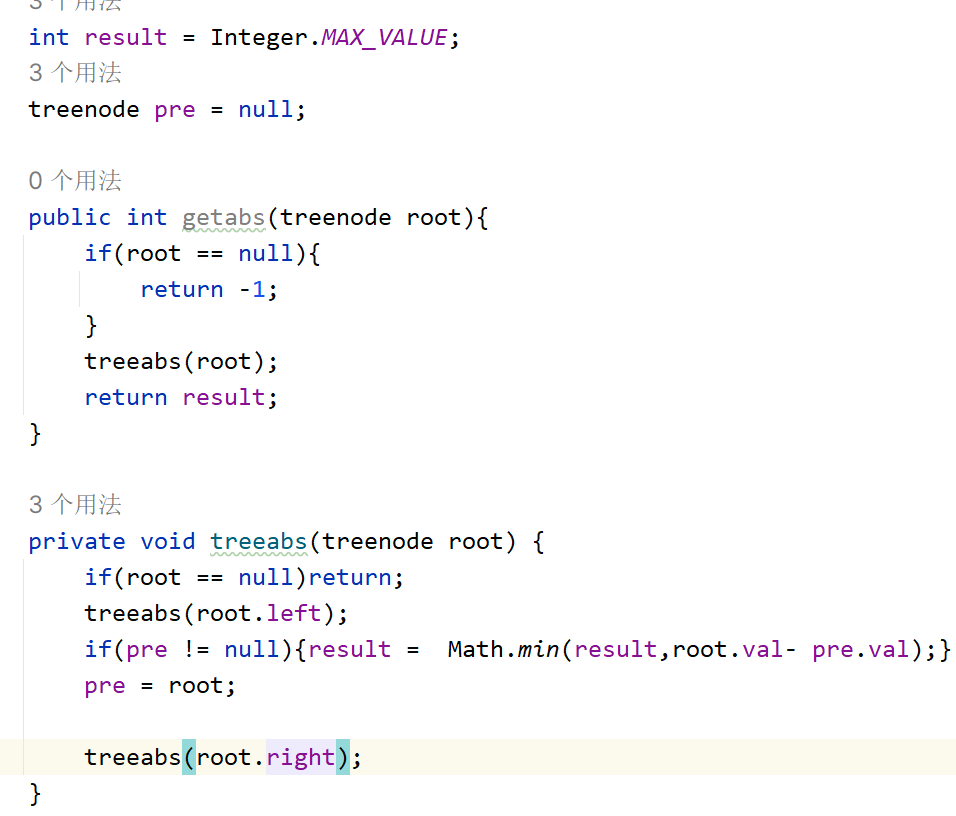
给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

• 思路： 递归加回溯，每次先递归左节点，然后跟新当前节点与上一节点的差值，回溯：将前一节点更新为当前节点，再递归右节点。

找二叉搜索树的众数

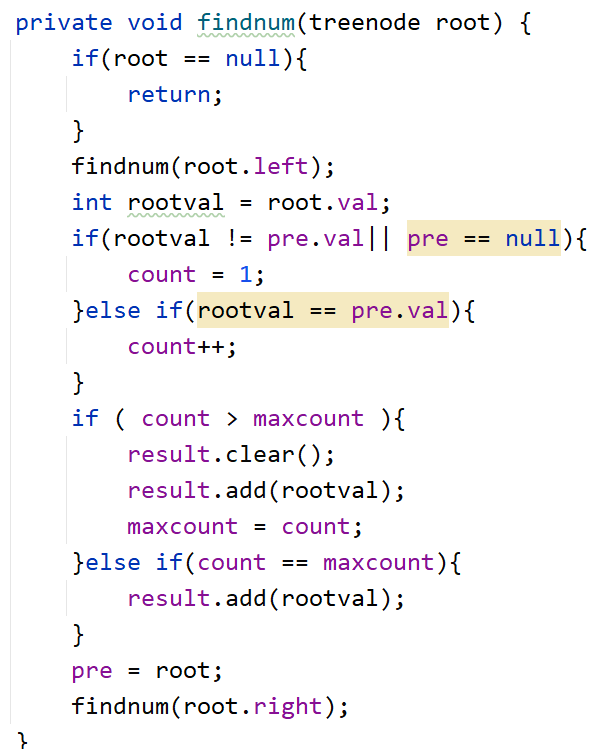
给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）

• 思路：遍历，每一个节点需要统计是否和上一个节点值相同，相同则更新count值，然后就是比较最大count值，有变化就更新众数列表，也就是
  清除再加入，或者直接加入（count值等于最大的时候）；

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

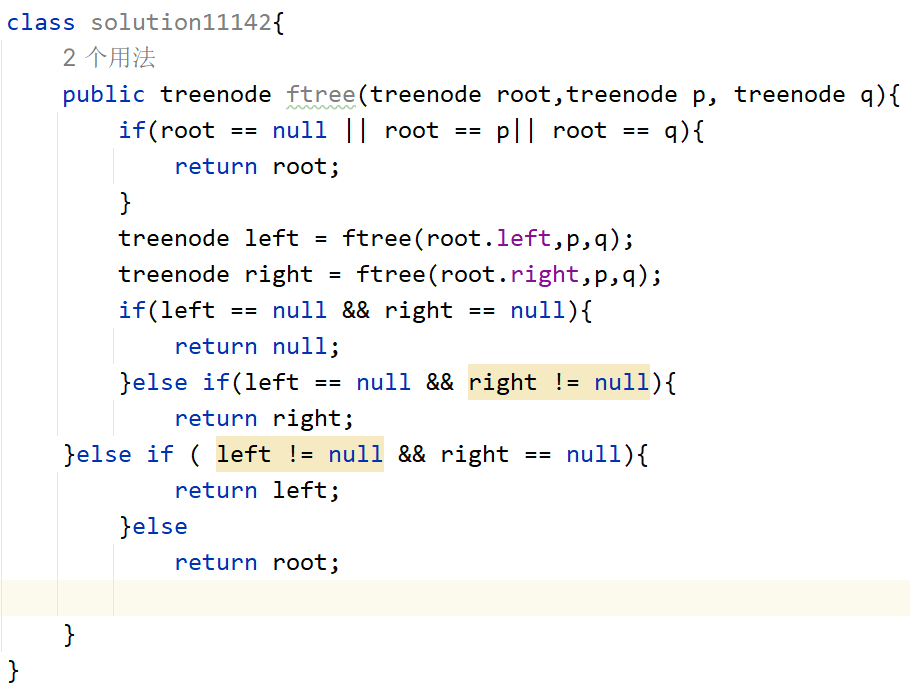
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

• 思路：递归，然后分左右，左右递归有一个值，递归终止条件是找到pq,或者节点值为空，只有一边有返回那一边的值即可，两边都有则返回它们的根节点。

二叉搜索树的最近公共祖先

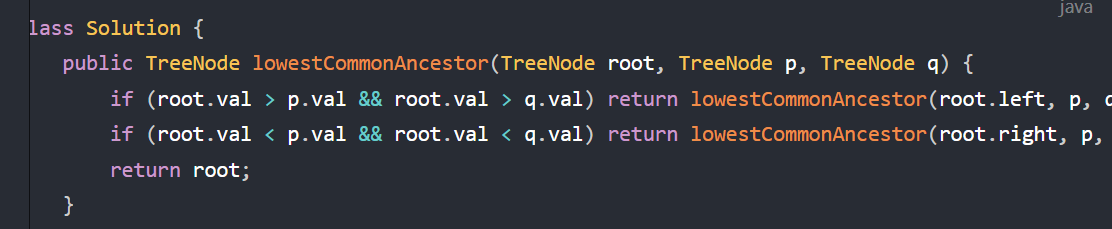
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

• 思路：因为是搜索树，所以自上而下的进行判断，根节点比目标节点都大的时候就遍历根节点的左节点，反之就是右节点，在中间的话就是祖先了。

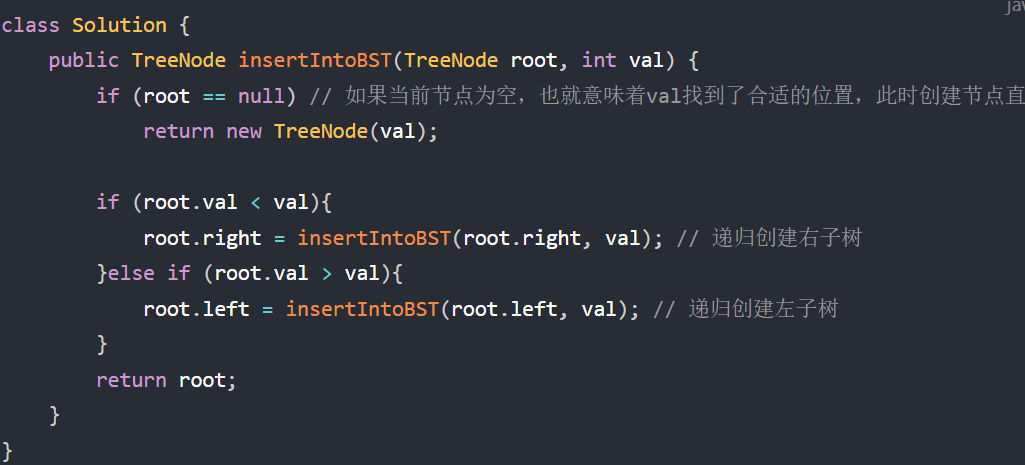
往二叉搜索树中插值

• 思路：还是递归，节点值大于目标值，就往左递归，反之往右，当节点值为空时，则找到了位置，在此位置创建即可

删除二叉搜索树的节点

• 思路：做判断，分为五种情况，每次返回删除节点的下一个节点，根据节点值和目标值进行判断，遍历左边还是右边。

修剪二叉树

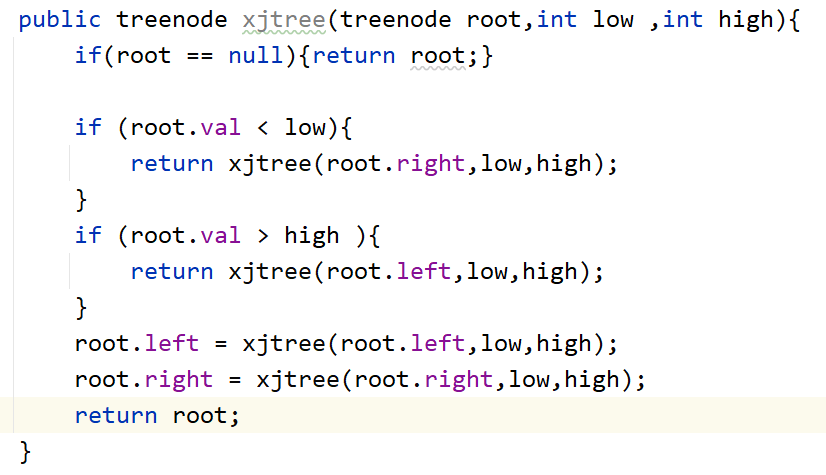
给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

• 思路：还是递归，当节点值小于最小值，传右节点到递归中，大于最大值传左节点，照此方法确定左右节点。

将有序数组转换为二叉搜索树

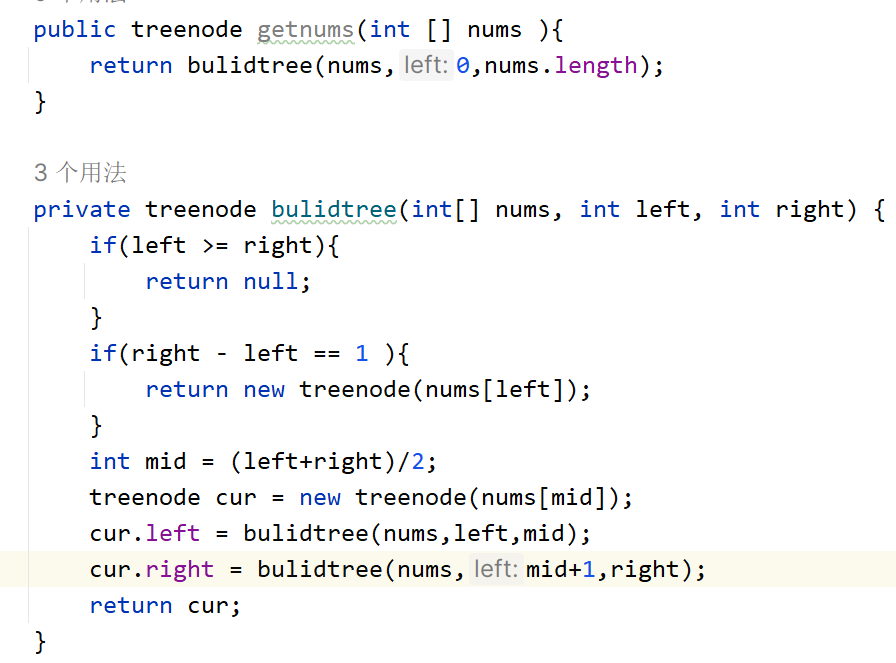
将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

• 思路：因为是有序数组，所以可以找到数组的中间值，然后节点的左右节点递归，当左右区间相差为1时，创建新节点，左区间大于右区间时，递归结束。

把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

• 思路：因为要求累加树也是搜索树，所以遍历的顺序为右中左，因此递归顺序也是先递归右，中间处理过程为将该节点的值加到总和上，并重置该节点的值为这个和，然后递归左边。